金属加工技術者 Dreamteam 株式会社酒井鉄工所

標準偏差とは、「平均値に対してどの位バラついているか」という意味です。
例えば、500個入りのガムを買って中身を調べた所、下の表のような結果が出ました。

平均値は同じ500です。
皆さんだったらどちらのお店で買います？
ギャンブル好きな人はＡ店かもしれませんが、ほとんどの人はＢ店で買いますよね。

なんでＢ店を選びましたか？
Ｂ店の方がバラツキの幅が少ないからですよね？

平均からの差を表にしてみます

偏差の合計

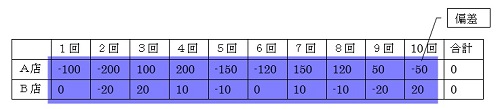
※ この平均からの差の事を偏差（平均の平と、差を合わせた言葉です！）と呼び合計は必ず0になります。

単純に偏差を求めても合計は0なのでＡ店、Ｂ店の違いは判りません。
ここで偏差を２乗すれば、必ずプラスになるので合計が0と言うことにはなりません。

偏差を2乗してみると

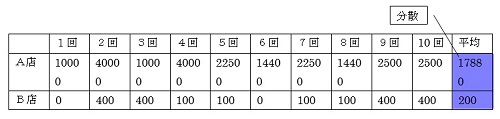
※この平均の事を分散と呼びます。
かなりの差が出ましたね。

この分散を２乗していたので元の状態に戻すために√の中に入れてみます。
Ａ店√17880=133.72
B店√200=14.14
Ａ店の数字が明らかに少ないですよね！この結果のことを標準偏差と呼びます。
Ａ店の標準偏差　133.72
B店の標準偏差　14.14

平均値が同じでも標準偏差にすると差は歴然ですね！
標準偏差の値が小さいほどバラツキが小さいということになります。

標準偏差の求め方は
① 平均を求める
② 偏差（平均との差）を求める
③ 分散（偏差の２乗した平均）を求める
④ 標準偏差（分散を√に入れる）を求める
以上の手順で標準偏差が求まります！

技能検定の特級では職種関係なく必ず覚えなくてはならないものです。挫折するとしたら品質管理かと思いますが、公式（Σやらなんやら）出てきますが計算の手順さえ覚えてしまえば公式は覚えなくてもいいです！数学の苦手な人でも正しい手順を踏めば計算できますのでチャレンジしてみてはいかがでしょう。

次回は、標準偏差の利用法（工程能力指数など）について書きたいと思います。